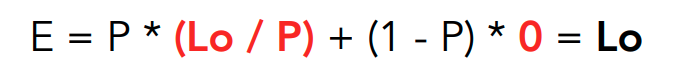对于Path Tracing中的最重要思想Russian Roulette & Importance Sampling,因为老是忘,所以这次尝试用更加简单无脑的语言总结一下。
Importance Sampling
先来说蒙特卡洛积分
传统的思想是黎曼积分,把每个小面积加起来,然后无限细分就会逼近真实值:
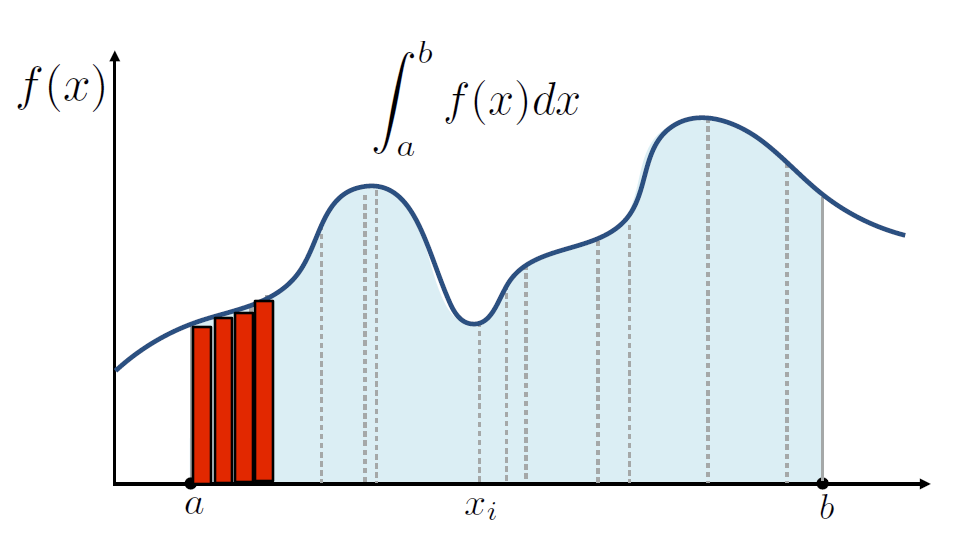
在定义域上均匀采样,采采采,每次都算整个定义域的面积,然后平均一下,随着采样数的增加,就可以逼近真实值,这是最简单的蒙特卡洛积分:
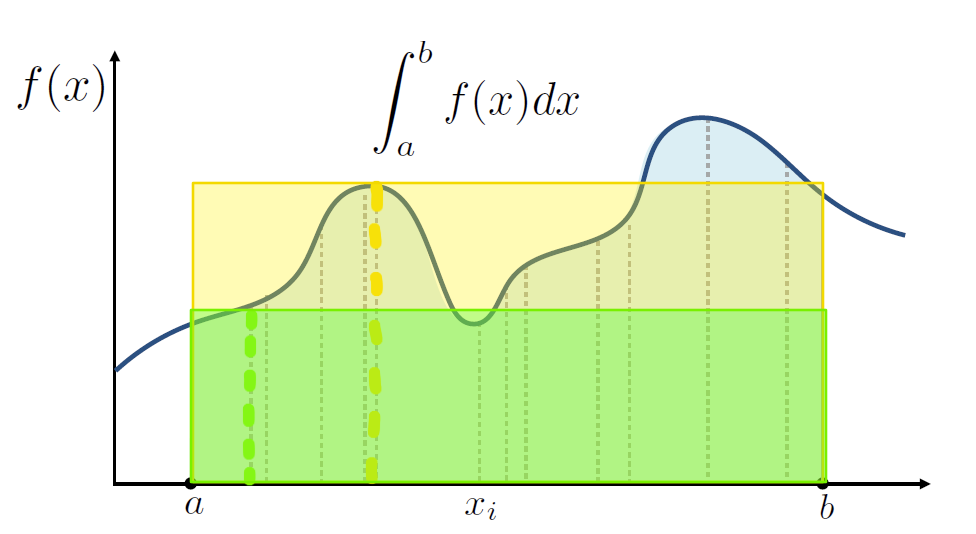
那么重要性采样是要解决一个什么问题呢?
引用一下我上一篇文章的话:
蒙特卡洛积分中,可以使用均匀采样和重要性采样。两种采样方式的积分结果期望是相同的,均随样本量的增加收敛于真实值,也就是说两种采样方式都是正确而无偏的。所以,重要性采样的目的在于,在同样的采样数下有效减少积分结果的方差,即积分结果更加收敛于真实值。
其实就是在比较少的采样数下,得到更逼近真实值的结果。
怎么做呢?
一个直观的想法是:多采值大的,少采值小的,就可以更快逼近。对应到Path Tracing中就是多采亮的地方,少采暗的地方,想想就觉得很对。
就像下图这样:
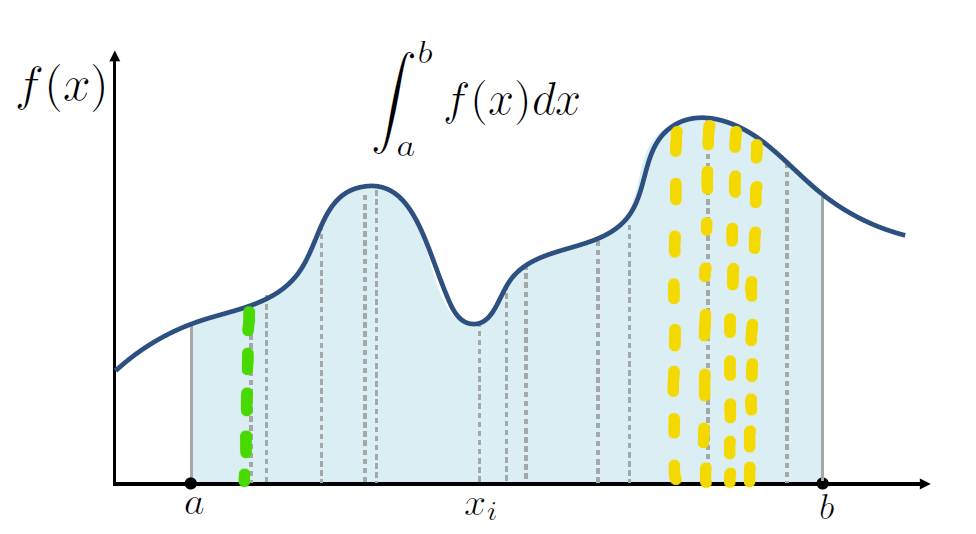
但是这样加起来的结果,直接平均明显不对,明显偏大,怎么办?很简单,把采样概率除掉再平均不就好了。
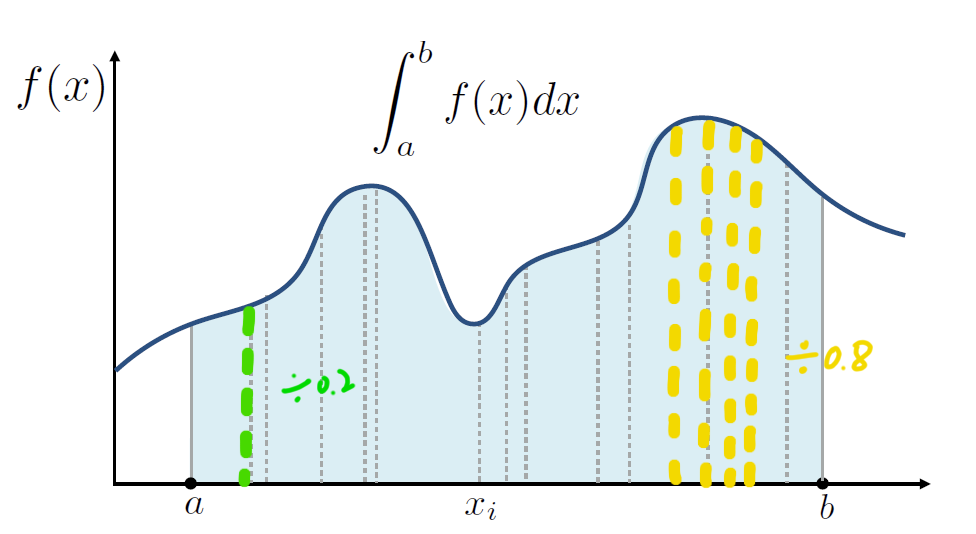
多采值大的,少采值小的这个思路是没问题了。
那么什么情况下逼近最快呢?想想应该是直接把原函数作为采样的PDF(概率密度函数)时是最理想的。
那么问题来了,我就是不知道原函数长啥样才用的蒙特卡洛积分啊。
(这步是我猜的)简单,先均匀采样一遍描出来个近似的函数,然后作为PDF扔进去不就行了,其实也差不了多少:
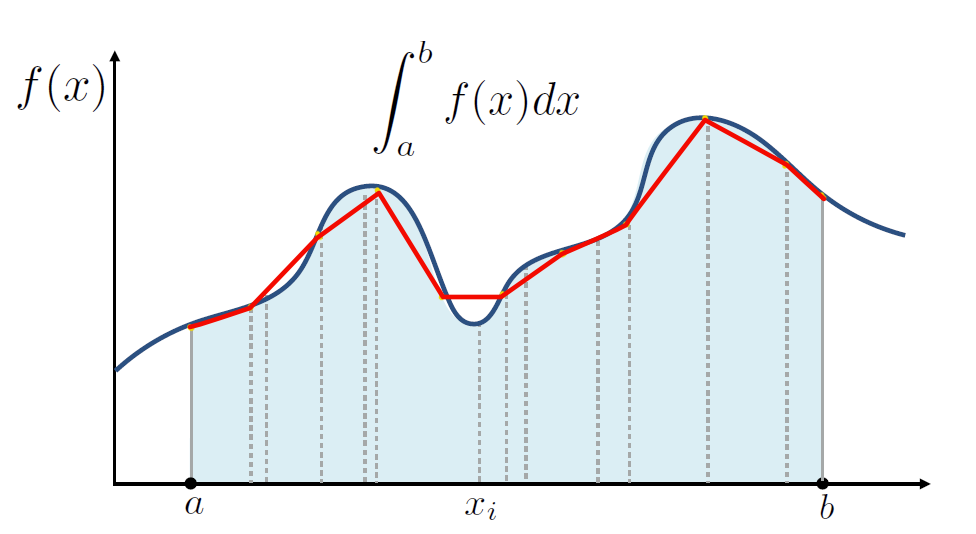
重要性采样就是这么简单。
Russian Roulette
下面我们要解决什么问题呢?
Path Tracing不知道什么时候停止追踪的问题。
当然我第一脑子肯定能想到,设置个阈值,能量小于0.0001的时候就停止,不就行了吗。
但是这样带来的渲染结果就是,总比真实值要暗那么一点点。(又不是不能用)
在Path Tracing中,理论上光线需要递归弹射无数次,我们无论怎样设置截断次数都将得到一个理论上不正确的值。
其实有更聪明的做法:
使用Russian Roulette可以非常巧妙的解决这一问题:对于一次光线弹射,设定以概率 $P$ 打出光线并计算结果,而概率 $1-P$ 不打出光线。将打出光线的计算结果除以 $P$ ,则其期望为理论正确值 $L_o$ 。对一次弹射而言这种处理毫无意义且引入误差,而对于多次计算则大不相同,对于同一条光线多次多层递归计算后的结果求期望,其结果依概率收敛于光线进行无穷次弹射的正确值。
对于一束光线,需要计算 $n$ 次弹射的概率为 $P^n$ ,随 $n$ 的增大而趋于零,这使得该递归算法总能终止。 $P$ 越小时算法终止越快,性能越好,计算结果随机误差越大;$P=1$ 时相当于原始思路,光线将会弹射无数次,递归算法无法终止。
完了,我自己写的我都看不懂,智商果真又下降了。
那么我们从头再来。
我们的目的是什么?让Path Tracing不会无限追踪下去,同时还能逼近真实值。
那么我们这样可以吗?每一步都以0.8的概率继续追踪,0.2的概率放弃追踪,这样追踪至少1次的概率为0.8,2次为0.64,3次为0.8 ^ 3,后面总有一次会停止追踪,无限追踪的概率为0。这不就解决了无限追踪的问题吗?我可真是个小机灵鬼。
但是这样一来,我们的结果不就远小于真实值了吗?
没关系,我们想想,多次采样后,我们的结果肯定就是真实值的大约0.8倍啊(其实不是,应该是小于0.8的一个值),再把0.8给他除掉不就行了。
仔细一想,明显不应该直接只在最后的结果上除,而是在每一步递归返回的结果上都要除,因为每一步都是0.8概率继续追踪。
完美。
对于一次采样的一次追踪而言,这样做明显是错的离谱,因为得到的要么是真实值的1 / 0.8 = 1.25倍,要么是0 / 0.8 = 0。但是对于大量采样,这样做的结果是1.25 * 0.8 + 0 * 0.2 = 1,绝了。
世界上怎么会有这么聪明的人,我好嫉妒。
学术点的说法是我以前写的:
这一方法成功将截断误差消除在是否打出光线的随机性中,系统误差化为随机误差,从而得到了正确无偏的值。
太妙了,总感觉这个思路将来可以用于解决其他问题。
总结
最后我发现了这两种方法共同的思路:
对于大量采样而言,先给它加个概率,然后再在结果中除掉不就行了。
希望我以后也能提出类似的方法,然后对自己说出:“我好聪明”。